The summer before my senior year, I found myself with a lot of free time on my hands from the absence of schoolwork. At the same time, I had been growing comfortable with using Houdini’s VEX, and was really enjoying the concept of breaking away from hard-coded nodes. As a result, I was incredibly bored and itching for a project where I’d be able to leverage these newfound skills. Also this summer, I had been killing a lot of time playing chess on my phone (I sucked at it).
Eventually I came up with the overly optimistic idea for a playable chess game within Houdini. In the project ideation phase, I imagined that I could also start learning about neural networks and implement an AI that would play back.
I would then spend the next two months working on building the base game, learning python and Houdini’s view states (yes, I started this project not even knowing basic python lol), studying machine learning fundamentals, training dozens of different NN architectures, reading academic thesis papers, and ultimately completing a real working chess game inside Houdini with a multilayer perceptron that plays back.

My first step was setting up the starting game board. Working off an 8x8 grid of points, I initially coded a constructor that would take an input FEN string and group points according to piece placement. This would be used for both the game backend as well as the visual aspect further down the pipeline. However, I painstakingly learned that a wrangle node’s point group changes occur only at the output. As a result, I would have been locked at a depth of 0 for all calculations as I could not loop over moves and perform code on the resultant boards.
I had previously also coded a transcription process that would take the point groupings and output a FEN string. I imagined I could use this with the constructor inside a solver to increment board changes throughout the game. As mentioned above, though, the depth locking would make this an unfavorable approach.
To get around this, I resorted to adjusting the constructor to instead create a 64-long detail string array attribute pertaining to piece placement. I would then manually loop over this array to perform any sort of calculations, rather than just running my wrangle node over points. As for the visual placement, I moved the point grouping mechanism to a wrangle node that would be executed after all backend calculations were done. This would create the groups from the detail attribute rather than the FEN directly, and only exist for the graphic purposes.
Additionally, I removed the transcription process entirely, as the solver could simply access the previous frame’s positions detail array. Effectively, I’d only be using the FEN string for the start frame/board, isolating the rest of the game to be run entirely within geometry attributes.
In hindsight, I could have foregone the transcription process even if I was still using point groups for the backend, but I’m glad I made this optimization nonetheless.
Adding in the piece movement was as simple as looping over the positions detail array and using these same point indexes to check for open spaces according to the piece type. There was a little complexity in the diagonals, but even that was just a matter of some tricky math and nesting the hell out of my loops. I saved these move sets as translation values within arrays at the point attribute level. For example, If a piece on space 34 could only move adjacently to the sides, point 34’s move set attribute would read [-1, +1].
Another interesting behavior that I had to program was ‘if the movement path is blocked, include the occupied end space in the move set if the occupying piece is an enemy (capturing the unit). If it is an ally, exclude it (blocked movement).’ This, also, was relatively easy to do - especially with the help of a duplicate detail array I made, which just carried the positions according to side rather than exact piece.
Then came the challenging part of the move set generation: culling moves based on checkmate. Essentially, if a move would expose or leave exposed the allied king, then that move is invalid and should be removed from the move set. In order to do this, I added another wrangle after the full unchecked move set construction that would iterate every single one of those moves and on the resultant board, create the next full move set. Instead of saving these secondaries though, I would add the attacked space indexes to arrays corresponding to each side’s vulnerabilities (again, per every move). At the end of a move’s vulnerability array generation, I would loop over this array to see if the allied king is within any of those vulnerable spaces. If it is, that move’s translation would be popped out of the piece’s move set.
Side note: This process is unoptimized. I’m currently adding depth to my move set generation that ideally wouldn’t be there. It would be much better to keep these invalid moves out of the move set from the beginning, rather than having to cull them later. However, this would be most easily done if my code thus far was more modular and used objects. However, since VEX doesn’t have object capabilities, and the lack of optimization in my code only has a depth cost of 1, I didn’t consider reworking this to be a priority.

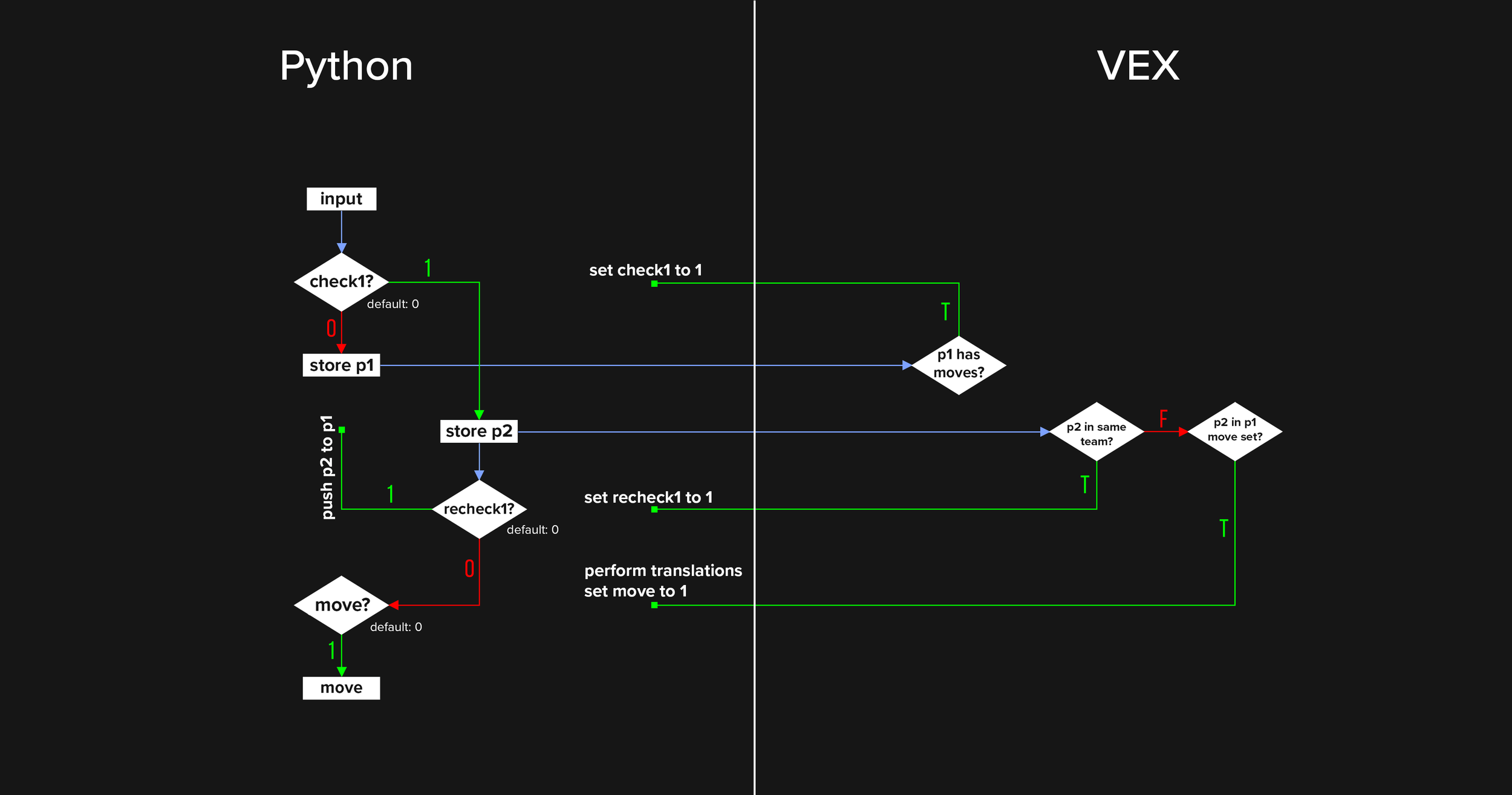
As for user input, I initially had no clue what to do. My first thought was that I could use changeable parameters that’d represent the moving piece’s index and the move’s index. In this way, a player could perform a move by changing these two parameters and then incrementing the frame manually. It wasn’t intuitive yet, but it worked.
Luckily though, when I had first begun working on this project, I messaged Peter Claes (of Infinity Ward) from my local community. I was mostly just telling him about the project because I thought the idea was really cool, but he ended up giving me some incredibly helpful guidance on this hurdle. He sent me a video from Paul Ambrosiussen (a name that I would stumble upon very often in my learning) that went over Houdini’s python viewer states. This was a feature that would make user input much more intuitive, but I had to learn python first.
With my precursor knowledge of Java/Javascript, picking up the python syntax was pretty straightforward. I just needed to adjust the setup so the input system would work by simply selecting a piece and an empty space. In order to do this properly however, there were many validation steps that I would have to program around. What would happen if the player selects a piece that cannot be moved - should the input system still interpret the next selection as the destination space? What if the next space they click is not in the available move set? What if they want to select a different piece than the one they initially selected? To address these circumstances, I set up a complex system of validation steps in VEX that would send confirmation checks back to python via node parameters. Effectively, my python and VEX scripts would ping back and forth in order to determine the destination of an input. When the conditions for a proper move are met, the frame is incremented automatically.
I made the validation system this way because the backend information of the game resided in Houdini and not in python’s memory. In hindsight, I could have just imported the relevant game information into python and set up the entire validation system there. While this would have been the most simple and elegant solution, it just wasn’t the one that came to mind, and luckily my choice of solution works just as well despite being much trickier to set up.
After this step, the game of chess was complete: A person could pass and play chess in Houdini. I had reached a milestone that I initially wasn’t sure was even possible.
At this point, I began watching dozens of hours worth of machine learning content. I explored how a neural network works with raw math before slowly diving into pytorch. To practice, I set up and practiced the typical MNIST image recognition model and played around with numerous different architectures. Once I felt comfortable with both the theory and the fundamentals, I began exploring numerous chess engines for training data, as well as common NN architecture for analyzing board games. I also looked into different theoretical ML approaches to the problem in general.
Eventually I decided on the theory I’d be using for my AI. I’d generate batches of random chess boards in python and convert each of them to bitboards of the shape [12, 8, 8]. Each of the 12 entries in the outermost layer would correspond to a piece type and the [8, 8] would represent an entire 8x8 chessboard. These tensors would be filled with either a 0 or 1 based on if a piece were present at a specific space or not. In this way, the tensor input for my model remains at a steady shape of [12, 8, 8] regardless of any variable elements. As for the output, I would need a single numerical value to train using stockfish’s cp score. Essentially, I’m approximating stockfish’s board analytics using a neural network.
To fit the context of my project, I added a wrangle node towards the end of my solver that iterates every move from the current board for the non-player side. For each of these moves, it loops over the positions array and appends a sequence of 12 bits to a string attribute on each point. As you might guess, these 12 bits represent a specific piece type on the respective point. For example, if the first 12 bits on point 3 are ‘000010000000’, there’s a white queen there. If the first 12 bits were ‘000000000010’ instead, then the space would conversely pertain to a black queen. Note that if only the first bits were read from point 0 to 63, then the result would be a tensor (after type conversions) corresponding to all the white pawns on the resultant board from the first possible move. The first 12 bits could similarly be converted to a tensor of the shape [12, 8, 8], representing the full board from one possible result of a move. By iterating every move, the code returns 64 strings of length 12n that get streamed to my python code and converted to a tensor of shape [n, 12, 8, 8] containing all possible boards. In this case, n represents the length of the entire move set available to the AI.

In python, I adjusted my code to perform a move after every move the player takes. If the AI is playing white, then it also plays once on state entrance, giving the AI the first move.
As for the process of performing a move, the code simply loads (upon startup) a state dictionary saved on my PC containing weights and biases from the model I’d end up training. Whenever the player has moved, It throws the tensor of possible boards’ bitboards into this loaded model and receives an output of shape [n]. Then, according to what side the AI is playing, either the highest or lowest score would be selected out of this array and its index would be sent back to VEX.
Note: Stockfish cp values center around 0 and are negative for black advantage or positive for white advantage. This is the reason why the AI-played side matters in terms of what score is chosen to be performed. I’d end up normalizing these values using a softmax function in generating my training data, but the principle remains the same.
After the AI’s move index is sent back to VEX, the moves are reiterated in the same order - this time with a counter. Once the counter matches the AI’s index, the source and destination points of the current move is sent through the same inputs as when a player performs a move. Because this is done directly within the code though, the input validation is not required and the process is much more straightforward. The frame will then be incremented once more, leading back to the player’s turn. I coded this recounting system this way because I wanted the game to perform the move directly from the move translations attribute on each point rather than recreate the board from the bitboard. I felt that compartmentalizing it this way would be best practice to minimize risk of error - If I were to make any changes and there was somehow something wrong with the bitboard, then the worst result would be that an suboptimal move would be chosen rather than having impossible moves occur. I never actually ran into any issues on this end, but regardless, good practice is good practice.

With everything else done, this is where the hard part began. Entirely outside of Houdini at this point, I needed to train a model and save its state dictionary for my code to load up.
To begin, I researched numerous different model formats that were common for chess AI. In this learning, the first model I had hope for was a residual network with 3 layers with 32 nodes each. These layers were activated by the ReLU() function and employed batch normalization in between every layer as well. I used Adam for the optimizer, and would come to find it outperforming all other optimizers consistently. Unfortunately though, the model plateaued in learning at a way-too-high loss value, and no amount of tweaking the architecture would fix it. I tried adjusting the activation functions, adding dropout layers, tweaking model shape, and even implementing adding of inputs - None of it helped.
The next big hope I had was in copying Alpha0’s structure. While there was very little specific information available on the neural network part of the engine, I found a lot of theory for it that worked as a solid lead. Essentially, Alpha0 works by having two outputs: a policy head and a value head. The policy head ties in with a Monte Carlo tree search for decision making, while the value head provides what seems like an analysis score for a specific choice of move. This similarity in analysis is what made me think Alpha0’s model would be a good starting point for my project - If I could emulate Alpha0’s model in the value head aspect, then I’d know my model has the capacity to ‘see’ complex game patterns. Unfortunately though, Alpha0 has 40 residual layers of 256 neurons each and this was far too much for my hardware to train. I tried to do it regardless of how incredibly slow it was, but the results didn’t actually seem like they were significantly better than the several other models I had tried.
Note that while these are the main promising leads I had, I tried dozens upon dozens of tweaks to these base models when they didn’t work out. Things were starting to seem grim.
Eventually, I found a couple academic papers that experimented with a different type of model: a multilayer perceptron. Of these, one paper approached chess AI in the exact same way I was handling it for my project: Using neural networks to approximate stockfish scoring. This was incredibly notable to me, because with all my previous attempts, I had to tweak the model I was imitating to fit my input/output formatting. As a result, any lack of performance I was seeing could be chalked up to improvisation error. This study removed that variable - if my model was still struggling, then it was due to an issue in my dataset or something else rather than the model itself. Despite having checked my data generation dozens of times previously, this ended up being the issue.

After troubleshooting the dataset a few more times, I finally found the problem. When I was scoring the boards with stockfish, the engine ‘mostly’ returned cp values. However, there were a few boards hidden in my dataset that were already in mate or draw conditions. These boards had been assigned mate scores of -1, 0, or 1. As it stood, boards that were heavily favored had cp scores as skewed as -1000 or 1000, but very similar boards also had mate scores of -1 or 1.
I addressed this inconsistency by normalizing the cp scores. I was then able to assign the mate boards values of 0 and 1, with draws being an even 0.5. I considered simply removing all the endgame boards from the dataset, but I wanted my model to have an understanding of these conditions as well.
After fixing this issue, the results of my training increased dramatically. Luckily, the study was very thorough in the training parameters used so I was able to emulate its conditions fairly easily and I also made some optimizations of my own. Ultimately, I was left with a model that finally trained decently.
The study also thoroughly compared the MLP model I was now using with the same residual networks I had tried and failed with before. Fortunately for me, it documented a clear trend in the MLP’s performing better. This meant that I didn’t have to retry all my previous attempts with my dataset fix in order to find the optimal model. The paper had already done so.
With this state dictionary saved out, I was finally done with my project. I had made the game of chess in Houdini, and implemented an AI that played back.
Looking back on this project, I recognize that there are things I could do much differently - and in some cases, much better. For starters, the dataset generation process opened my eyes to how convenient python is, especially considering all the libraries that are readily available. If this project was meant to be an actual production-oriented HDA rather than a proof of concept, I could easily outsource the entire backend to python’s chess library. As for AI support, I could just have stockfish handling it instead of trying to implement a machine learning approximation. In fact, If I was to redo this project using these alternative options, I could probably set up the entire game within an hour. With that being said however, I started this project for a difficult -albeit gimmicky- challenge, and for a learning opportunity. Most importantly, I made this for fun. With these project goals in mind, I’m ultimately very glad I approached it this way.
The other main thing that I’d have liked to do a lot better is my AI model itself. Closely (but not exactly) mirroring the academic paper I found, I was able to get a resulting AI that feels, at the very least, slightly intelligent. I trained it using a stockfish Elo of 2500 with a depth of 2 in order to make the training process a lot more simple. Because of this however, the model lacks the ability to ‘see’ complex patterns far into the future that a human player would more easily notice. As a result, captures are prioritized but win conditions aren’t ‘seen’ or played towards. This makes sense too, considering the methodology of the training data used.
Additionally, the softmax normalization of the training stockfish scores results in the model viewing heavily skewed boards as more similar than they really are. It’d be able to easily discern a good move from a bad one, but struggle to consistently differentiate between a good move and a better one. This, again, leads to blunders being punished but there still remains no particular strategy.
Lastly, the results of my model fitting were somewhat similar to the paper’s model. Despite this though, the loss values in the study were never actually great either. The paper itself confirmed this in their results, as the authors noticed that while good moves were chosen, ideal moves were not played with consistency. I reached out to the authors with questions I had about their approach in attempts of improving the results, but I unfortunately never received a reply.
With all these things considered, I’d expect the Elo of my model to hover around 500 - far from the original 2500 that the model was trained at. While I’d really like to improve this, I noticed diminishing returns in my attempts and would probably have to redesign the theory surrounding my AI entirely. However, I had already reached all the goals I had for this project, and don’t consider this a priority. With everything said and done, this was fully working and I had accomplished exactly what I had ideated.